Question

A regression and correlation analysis resulted in the following information regarding a dependent variable ( y) and an independent variable ( x). Σx = 90 Σ(y - )(x - ) = 466 Σy = 170 Σ(x - )2 = 234 n = 10 Σ(y - )2 = 1434 SSE = 505.98 ​ The sum of squares due to regression (SSR) is

Answer 1

The sum of squares due to regression(SSR)=928.02

Explanation:

We are given that

Dependent variable=y

Independent variable=x

`\sum x=90`

`\sum(y-\bar y)(x-\bar x)=466`

`\sum y=170`

`\sum(x-\bar x)^2=234`

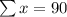
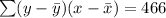
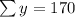
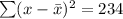
n=10

`\sum(y-\bar y)^2=1434`

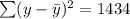
SSE=505.98

We have to find the sum of squares due to regression.

It means we have to find SSR.

SST=
`\sum(y-\bar y)^2=1434`

`SSR=SST-SSE=1434-505.98=928.02`

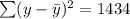
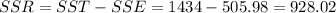
Hence, the sum of squares due to regression(SSR)=928.02