Answer:
22m
Explanation:
Let height of flagpole=h
AB==17 m
 (1 degree= 60 minute)
(1 degree= 60 minute)
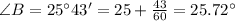
We have to find the approximate height of the flagpole.
In triangle CDA,

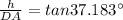
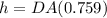
In triangle CDB,
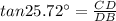
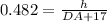
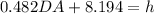
Substitute the value
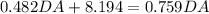
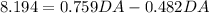
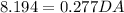
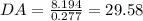
Substitute the value
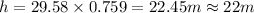
Hence, the height of the flagpole=22 m