Question

Exponential function f(x) has a y intercept of 3 and an x intercept of -2. the function is always increasing as the value of x increases, but the function never reaches y=4

would it be decreasing or increasing and will it point down or up?
PLZ ANSWER ASAP

Answer 1

`f(x)=-\left((1)/(2)\right)^x+4`

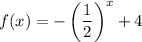
The exponential function is increasing and is concave down

Explanation:

Let the equation of exponential function be

`f(x)=a\cdot b^x+c,\ ,\ b>0`

1. Exponential function f(x) has a y intercept of 3, so the graph of f(x) passes through the point (0,3). Thus,

`3=a\cdot b^0+c\\ \\3=a+c`

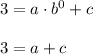
2. Exponential function f(x) has an x intercept of -2, so the graph of f(x) passes through the point (-2,0). Thus,

`0=a\cdot b^(-2)+c\\ \\0=(a)/(b^2)+c`

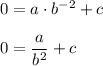
3. Function is always increasing as the value of x increases, but the function never reaches y=4, so

`c=4`

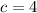
Hence,

`\left\{\begin{array}{l}a+4=3\\ \\(a)/(b^2)+4=0\end{array}\right.\Rightarrow \left\{\begin{array}{l}a=-1\\ \\(-1)/(b^2)+4=0\end{array}\right.\Rightarrow \left\{\begin{array}{l}a=-1\\ \\b^2=(1)/(4)\end{array}\right.`

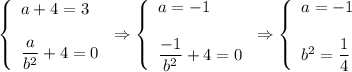
So,

`a=-1,\\ \\b=(1)/(2),\\ \\c=4,\\ \\f(x)=-\left((1)/(2)\right)^x+4`