Question

A satellite is put into an elliptical orbit around the Earth. When the satellite is at its perigee, its nearest point to the Earth, its height above the ground is hp=227.0 km, and it is moving with a speed of vp=8.950 km/s. The gravitational constant G equals 6.67×10−11 m3·kg−1·s−2 and the mass of Earth equals 5.972×1024 kg.When the satellite reaches its apogee, at its farthest point from the Earth, what is its height ha above the ground?

Answer 1

6633549.52903 m

Step-by-step explanation:

G = Gravitational constant = 6.67 × 10⁻¹¹ m³/kgs²

m = Mass of the Earth = 5.972 × 10²⁴ kg

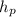`h_p` = Height above ground = 227 km

`v_p` = Velocity at perigee = 8.95 km/s

Perigee distance is

`R_p=6371+227=6598\ km`

The apogee distance is given by

`R_a=(R_p)/((2Gm)/(R_pv_p^2)-1)\\\Rightarrow R_a=(6598* 10^3)/((2* 6.67* 10^(-11)* 5.972* 10^(24))/(6598* 10^3* (8.950* 10^3)^2)-1)\\\Rightarrow R_a=13004549.52903\ m`

The height above the ground would be

`h_a=13004549.52903-6371000=6633549.52903\ m`

The height above the ground is 6633549.52903 m