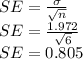Question

Te professor of a large calculus class randomly selected 6 students and asked the amount of time (in hours) spent for his course per week. Te data are given below. 10 8 9 7 11 13

a. Estimate the mean of the time spent in a week for this course by the students who are taking this course.
b. Estimate the standard deviation of the time spent in a week for this course by the students who are taking this course.
c. Estimate the standard error of the estimated mean time spent in a week for this course by the students who are taking this course.

Answer 1

a. μ = 9.667 hours

b. σ = 1.972 hours

c. SE = 0.805 hours

Explanation:

Sample size (n) = 6

Sample data (xi) = 10, 8, 9, 7, 11, 13

a. Mean time spent in a week for this course by students:

Sample mean is given by:

`\mu = (\sum x_i)/(n) \\\mu = (10+9+7+11+13)/(6)\\\mu=9.667`

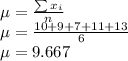
Mean time spent in a week per student is 9.667 hours

b. Standard deviation of the time spent in a week for this course by students:

Standard deviation is given by:

`\sigma = \sqrt{(\sum(x_i - \mu)^2)/(n)}\\\sigma = \sqrt{((10- 9.667)^2+(8- 9.667)^2+(9- 9.667)^2+(7- 9.667)^2+(11- 9.667)^2+(13- 9.667)^2)/(6)}\\\sigma =1.972`

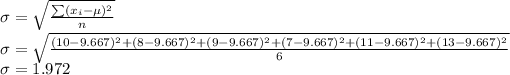
c. Standard error of the estimated mean time spent in a week for this course by students:

Standard error is given by:

`SE = (\sigma)/(\sqrt n)\\SE = (1.972)/(\sqrt 6)\\SE=0.805`