Question

At 6:00 PM, a flagpole that is 35 feet tall casts a shadow that is 50 feet long. At the same time, how long will a person's shadow be if they are 4 feet tall?

Please help ASAP!!! :(

Answer 1

The length of the person’s shadow is 5.7ft

Step-by-step explanation:

Length of the flagpole =a= 35ft

Length of the shadow of the flagpole= b=50ft

Length of the person=c= 4ft

Suppose the length of the person’s shadow is=d

According to the rules of trigonometry

`\frac{\text { Length of the flagpole }}{\text { Length of the shadow of the flagpole }}=\frac{\text { Length of the person }}{\text { Length of the person's shadow }}`

`(a)/(b)=(c)/(d)`

`(35)/(50)=(4)/(d)`

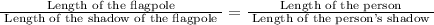
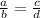
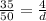
35d=200

d=
`(200)/(35)`

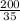
d=5.7ft

Hence, The length of the person’s shadow is 5.7ft.