Question

In an oscillating L C circuit, the maximum charge on the capacitor is 1.5 × 10 − 6 C and the maximum current through the inductor is 5.5 mA.

(a) What is the period of the oscillations?
(b) How much time elapses between an instant when the capacitor is uncharged and the next instant when it is fully charged?

Answer 1

T= 1.71×10^{-3} sec= 1.71 mili sec

t_{fc}= 4.281×10^{-4} sec or 0.4281 mili sec

Step-by-step explanation:

First of all we write equation for current oscillation in LC circuits. Note, the maximum current (I_0)= 5.5 mA is the amplitude of this function. Then, we continue to solve for the angular frequency(ω). Afterwards, we calculate the time period T. qo = maximum charge on capacitor. = 1.5× 10 ^− 6 C

a) I(t) = -ωqosin(ωt+φ)

⇒Io= ωqo

⇒ω= Io/qo

also we know that T= 2π/ω

⇒T=
`2\pi(q_0)/(I_0)`

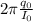
now putting the values we get

=
`2\pi(1.5*10^(-6))/(5.5*10^(-3))`

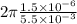
= 1.71×10^{-3} sec

b) note that the time
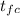`t_(fc)` it takes the capacitor to from uncharge to fully charged is one fourth of the period . That is

`t_(fc)= (T)/(4)`

`t_(fc)= ( 1.71*10^(-3) )/(4)`

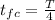
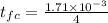
t_{fc}= 4.281×10^{-4} sec or 0.4281 mili sec