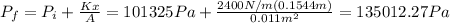Question

A cylinder is closed by a piston connected to a spring of constant 2.40 103 N/m. With the spring relaxed, the cylinder is filled with 5.00 L of gas at a pressure of 1.00 atm and a temperature of 20.0°C.

(a) If the piston has a cross-sectional area of 0.0110 m2 and negligible mass, how high will it rise when the temperature is raised to 250°C? m
(b) What is the pressure of the gas at 250°C?

Answer 1

a) The correct solution would be x=0.1544m.

b)
`P_f = P_i +(Kx)/(A)=101325Pa +(2400N/m (0.1544m))/(0.011m^2)=135012.27 Pa`

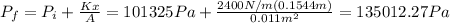
Step-by-step explanation:

Initial states

`P_i =1atm=101325 Pa` represent the initial pressure

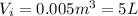`V_i =0.005m^3 = 5L` represent the initial volume

N represent the number of moles

`T_i = 20+273.15=293.15K` represent the initial temperature

Final states

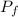`P_f` represent the final pressure

`V_f` represent the final volume

`T_f = 250+273.15=523.15K`

Part a

From the initial states and with the law of ideal gases we can find the moles like this

`n=(P_iV_i)/(RT_i)=(101325Pa(0.005m^3))/(8.314(J)/(mol K) 293.15K)=0.2079mol`

In order to find the final pressure we need to take in count the atmospheric pressure and the pressure related to the force that the springs applies to the piston, like this:

`P_f =P_i +(F)/(A)= P_i +(Kx)/(A)`

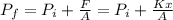
Where x is the distance that the piston is displaced upward, since increase the temperature and the gas inside tends to expand.

And we can find the final volume on this way
`V_f = V_i + Ax`

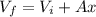
For the final state we have the following equation:

`P_f V_f=nR T_f`

And if we replace
`V_f` we got:

`(P_i +(Kx)/(A))(V_i +Ax)=nRT_f`

`P_i V_i +P_i A x +(KxV_i)/(A)+kx^2=nRT_f`

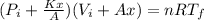
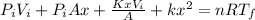
And x can be solved with a quadratic equation:

`kx^2+(P_i A +(V_i K)/(A))x+(P_i V_i-nRT_f)=0`

`2400 k^2 +(101325Pa)(0.0110m^2)+(0.005m^3 x2400N/m)/(0.0110m^2))x+(101325Pa(0.005m^3)-0.2079mol(8.314J/molK)(523.15K))=0`

`2400 k^2 +(2205.484)x-397.63=0`

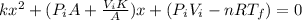
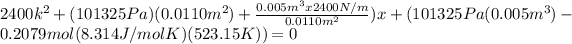
And solving for x we got x=0.1544 or x=-1.07331 m. The correct solution would be x=0.1544m.

Part b

And the final pressure would be given by:

`P_f = P_i +(Kx)/(A)=101325Pa +(2400N/m (0.1544m))/(0.011m^2)=135012.27 Pa`