Answer:
Option A is correct.
i.e. x = 1, x = 0 is an extraneous solution.
Explanation:
Given the expression
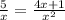
Solving the rational function
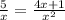
Apply fraction across multiply: if
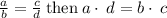
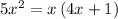
Subtract x(4x+1) from both sides
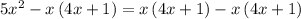
Simplify
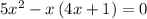
5x² - 4x² - x = 0
x² - x = 0
Factor x² - x = x(x-1)
so
x(x-1) = 0
Using the zero factor principle
if ab=0, then a=0 or b=0 (or both a=0 and b=0)

Thus, the solution to the equation is:

But, it is clear that if we substitute x = 0, the equation becomes undefined because we can not have the denominator to be 0.
In other words, the equation is undefined for x = 0
Thus, x = 0 is an extraneous solutions.
Therefore, option A is correct.
i.e. x = 1, x = 0 is an extraneous solution.