Answer:
Frequency, f = 3.35 Hz
Step-by-step explanation:
It is given that,
Mass of the object, m = 8 kg
Stretching in the spring, x = 2.2 cm
When the spring is hanged up in the Earth's gravitational field, its weight is balanced by the force in the spring. So,
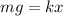
k is the spring constant
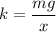
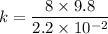
k = 3563.63 N/m
Let f is the frequency of oscillation. Its expression is given by :
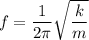

f = 3.35 Hz
So, the frequency of oscillation by the spring is 3.35 Hz. Hence, this is the required solution.