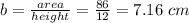Question

if the area of a parallelogram is 86cm and the height is 12cm write an equation that relates the height,base and area of the parallelogram

Answer 1

The relation to find base is,
`base=(area\ of\ the \ parallelogram)/(height)=(86)/(12)=7.16\ cm`

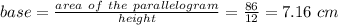
Explanation:

Given

Area of the parallelogram
`=86\ cm^2`

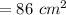
Height of the parallelogram
`=12\ cm`

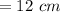
We know that the area of the parallelogram
`=base* height`

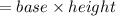
So

To find base we have to divide the height on both sides of the equation.

`base=(area\ of\ the \ parallelogram)/(height)`

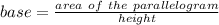
Plugging the values.

`base=(86)/(12) =7.1\ cm`

So the base in terms of area of the parallelogram and its height is
`b=(area)/(height) =(86)/(12)=7.16\ cm`