Question

1. If we place a box of 200 Kg on incline plane of 30 degree, does the weight of box and normal force are equal and opposite to each other.

Answer 1

The weight on the box and the normal force on the box will not be exactly opposite to one another. The angle between these two forces will be
`150^\circ`.

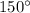If the box isn't moving:

`\begin{aligned}& \text{normal force} \\ &= \cos\left(30^\circ\right) \cdot \text{weight} \\ &= (√(3))/(2) \cdot \text{weight}\end{aligned}`.

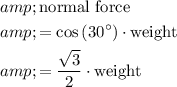Step-by-step explanation:

The weight on an object on the surface of the earth should always point downwards towards the center of the planet.

On the other hand, as the name suggest, the normal force on an object is normal to the surface that exerted this normal force. In this question, that surface is a plane with a
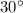`30^\circ` incline to the ground. The corresponding normal force will be at
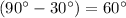`\left(90^\circ - 30^\circ\right) = 60^\circ` above the ground.

The angle between the normal force (
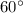`60^\circ` above the ground) and the weight (vertically downwards toward the ground.) would be
`\left(60^\circ + 90^\circ\right) = 150^\circ`.

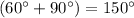How could the box possibly not move even though the normal force on it isn't exactly opposite to its weight? Refer to the second diagram (not to scale) attached; decompose the weight on the box into two components:

• The first component is normal to the incline.
• The second component is parallel to the incline.

Notice how the original weight and the two decomposed forces form a right triangle.

Component normal to the incline:
`\displaystyle \left(\cos\left(30^\circ \right)\right) \cdot \text{weight} = (√(3))/(2)\cdot \text{weight}`.

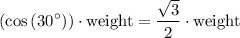Component parallel to the incline:
`\displaystyle \left(\sin\left(30^\circ \right)\right) \cdot \text{weight} = (1)/(2)\cdot \text{weight}`.

Notice that the vector sum of these two components is equal to the downward weight before the decomposition.

The normal force would be opposite to the component of the weight that is normal to the incline.The two forces should be equal in size. Therefore, the magnitude of the normal force should also be
`\displaystyle \left(\left.√(3)\right/ 2\right)\cdot \text{weight}`.

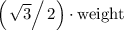If the box is at equilibrium, then the friction on this box (parallel to the incline) should be equal in size to the component of weight that is parallel to the incline.