Question

The cell potential of the following electrochemical cell depends on the gold concentration in the cathode half-cell:________

Pt(s)
|H2(g,1atm)
|H+(aq,1.0M)
|Au3+(aq,?M)
|Au(s).
What is the concentration of Au3+ in the solution if Ecell is 1.23 V ?

Answer 1

Answer: The concentration of
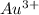`Au^(3+)` is
`1.096* 10^(-6)`

Step-by-step explanation:

The given chemical cell follows:

`Pt(s)|H_2(g,1atm)|H^+(aq,1.0M)||Au^(3+)(aq,?M)|Au(s)`

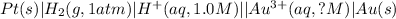
Oxidation half reaction:
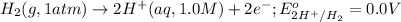`H_2(g,1atm)\rightarrow 2H^(+)(aq,1.0M)+2e^-;E^o_(2H^(+)/H_2)=0.0V` ( × 3)

Reduction half reaction:
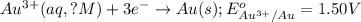`Au^(3+)(aq,?M)+3e^-\rightarrow Au(s);E^o_(Au^(3+)/Au)=1.50V` ( × 2)

Net cell reaction:
`3H_2(g,1atm)+2Au^(3+)(aq,?M)\rightarrow 6H^(+)(aq,1.0M)+2Au(s)`

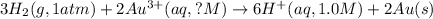
Oxidation reaction occurs at anode and reduction reaction occurs at cathode.

To calculate the
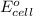`E^o_(cell)` of the reaction, we use the equation:

`E^o_(cell)=E^o_(cathode)-E^o_(anode)`

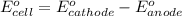
Putting values in above equation, we get:

`E^o_(cell)=1.50-(0.0)=1.50V`

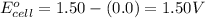
To calculate the EMF of the cell, we use the Nernst equation, which is:

`E_(cell)=E^o_(cell)-(0.059)/(n)\log ([H^(+)]^6)/([Au^(3+)]^2)`

where,

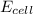`E_(cell)` = electrode potential of the cell = 1.23 V

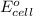`E^o_(cell)` = standard electrode potential of the cell = +1.50 V

n = number of electrons exchanged = 6

`[H^(+)]=1.0M`

`[Au^(3+)]=?M`

Putting values in above equation, we get:

`1.23=1.50-(0.059)/(6)* \log(((1.0)^6)/([Au^(3+)]^2))`

`[Au^(3+)]=-1.0906* 10^(-6),1.096* 10^(-6)`

Neglecting the negative value because concentration cannot be negative.

Hence, the concentration of
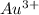`Au^(3+)` is
`1.096* 10^(-6)`