Answer:
a)
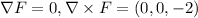
b)
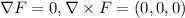 ,
,
 .
.
c)

Explanation:
Remember, if F= <f,g,h> is a vector field and
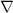 is the operator
is the operator
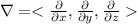
- the divergence of F is
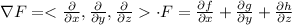
- the curl of F is
![\\abla* F=det(\left[\begin{array}{ccc}i&j&k\\(\partial)/(\partial x)&(\partial)/(\partial y)&(\partial)/(\partial z)\\f&g&h\end{array}\right] )](https://img.qammunity.org/2020/formulas/mathematics/college/fg4oob90li9ylrdsqfnozgqb1ebhoilhof.png)
a)
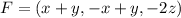
The divergence of F is
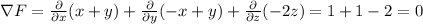
The curl of F is
![\\abla* F=det(\left[\begin{array}{ccc}i&j&k\\(\partial)/(\partial x)&(\partial)/(\partial y)&(\partial)/(\partial z)\\x+y&-x+y&-2z\end{array}\right])\\=i((\partial)/(\partial y)(-2z)-(\partial)/(\partial z)(-x+y))-j((\partial)/(\partial x)(-2z)-(\partial)/(\partial z)(x+y))+k((\partial)/(\partial x)(-x+y)-(\partial)/(\partial y)(x+y))=0i-0j-2k=(0,0,-2)](https://img.qammunity.org/2020/formulas/mathematics/college/ti8vv4f928m36j0hsvjn6ujqx9el2dynof.png)
b)
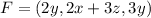
The divergence of F is

The curl of F is
![\\abla* F=det(\left[\begin{array}{ccc}i&j&k\\(\partial)/(\partial x)&(\partial)/(\partial y)&(\partial)/(\partial z)\\2y&2x+3z&3y\end{array}\right])\\=i((\partial)/(\partial y)(3y)-(\partial)/(\partial z)(2x+3z))-j((\partial)/(\partial x)(3y)-(\partial)/(\partial z)(2y))+k((\partial)/(\partial x)(2x+-3z)-(\partial)/(\partial y)(2y))=0i-0j+0k=(0,0,0)](https://img.qammunity.org/2020/formulas/mathematics/college/jyije0kfok438r7uo0ymyuc3wlml4lkyay.png)
Since the curl of F is 0 the we will try find f such that the gradient of f be F.
Since
 ,
,
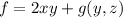 .
.
Since
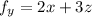 ,
,
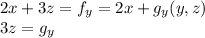 .
.
Since
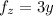 and
and
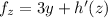 , then
, then
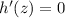 . Thins means that
. Thins means that
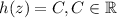
Therefore,
 .
.
c)
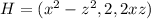
The divergence of F is
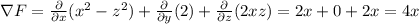
The curl of F is
![\\abla* F=det(\left[\begin{array}{ccc}i&j&k\\(\partial)/(\partial x)&(\partial)/(\partial y)&(\partial)/(\partial z)\\x^2-z^2&2&2xz\end{array}\right])\\=i((\partial)/(\partial y)(2xz)-(\partial)/(\partial z)(2))-j((\partial)/(\partial x)(2xz)-(\partial)/(\partial z)(x^2-z^2))+k((\partial)/(\partial x)(2)-(\partial)/(\partial y)(x^2-z^2))=0i-(2z-(-2z))j-0k=(0,-4z,0)](https://img.qammunity.org/2020/formulas/mathematics/college/nvkxhbrzcv0alc23rbilelfwmoxc89bvfh.png)