Question

In the year 2006, a company made $7 million in profit. For each consecutive year after that, their profit increased by 9%. How much would the company's profit be in the year 2008, to the nearest tenth of a million dollars?

Answer 1

The company's profit be in the year 2008 is $8.3 million.

Explanation:

Given:

In the year 2006, a company made $7 million in profit, their profit increased by 9%.

So, we need to calculate the company's profit be in the year 2008.

Now, by putting the formula to find the profit(P) after the two year:

Difference between the year = 2008 - 2006 = 2 year.

So, number of years(n) = 2 year

Rate of profit increasing(r) = 9%

Amount company made in 2006 (A) = $7 million.

`P=A(1+(r)/(100))^(n)`

`P=7(1+(9)/(100))^(2)`

`P=7(1+0.09)^(2)`

`P=7(1.09)^(2)`

`P=7* 1.188`

`P=8.316`

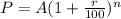
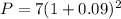
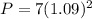
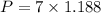
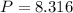
Profit in the year 2008 would be 8.316 million, and nearest to the tenth of a million dollars is $8.3 as 3 is in the tenth place of the decimal and 1 in the hundredth so rounding will change $8.316 to $8.3.

Therefore, the company's profit be in the year 2008 is $8.3 million.