Step-by-step explanation:
First, we will calculate the molar mass of
 as follows.
as follows.
Molar mass of
 =
=
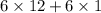
= 78 g/mol
So, when 2 mol of
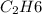 burns, then heat produced = 6542 KJ
burns, then heat produced = 6542 KJ
Hence, this means that 2 molecules of
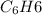 are equal to
are equal to
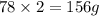 of
of
 burns, heat produced = 6542 KJ
burns, heat produced = 6542 KJ
Therefore, heat produced by burning 5.5 g of
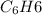 =
=

= 228.97 kJ
= 228970 J (as 1 kJ = 1000 J)
It if given that for water, m = 5691 g
And, we know that specific heat capacity of water is 4.186
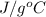 .
.
As, Q =
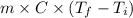
228970 J =
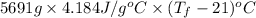
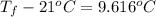

Thus, we can conclude that the final temperature of the water is
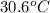 .
.