Answer:
 and
and

Explanation:
Assume that the terminal side of thetaθ passes through the point (−12,5).
In ordered pair (-12,5), x-intercept is negative and y-intercept is positive. It means the point lies in 2nd quadrant.
Using Pythagoras theorem:
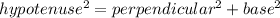
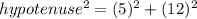
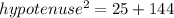
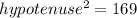
Taking square root on both sides.
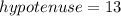
In a right angled triangle
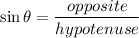

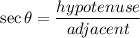
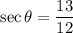
In second quadrant only sine and cosecant are positive.
 and
and
