Answer:
0.25938 W
Step-by-step explanation:
c = Speed of light =
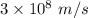
 = Frequency = 3 GHz
= Frequency = 3 GHz
d = Diameter of lossless antenna = 1 m
r = Radius =
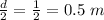
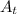 = Area of transmitter
= Area of transmitter
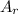 = Area of receiver
= Area of receiver
R = Distance between the antennae = 40 km
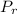 = Power of receiver =
= Power of receiver =
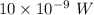
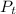 = Power of Transmitter
= Power of Transmitter
Wavelength
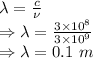
From Friis transmission formula we have
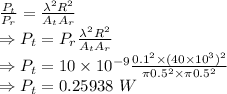
The power that should be transmitted is 0.25938 W