Question

(1+tanx)/(sinx+cosx)=secx

Answer 1

`(1+\tan x)/(\sin x+\cos x)=\sec x` is proved

Solution:

Given that,

`(1+\tan x)/(\sin x+\cos x)=\sec x` ------- (1)

First we will simplify the LHS and then compare it with RHS

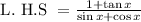`\text { L. H.S }=(1+\tan x)/(\sin x+\cos x)` ------ (2)

`\text {We know that } \tan x=(\sin x)/(\cos x)`

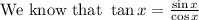
Substitute this in eqn (2)

`=(1+(\sin x)/(\cos x))/(\sin x+\cos x)`

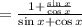
On simplification we get,

`=((\sin x+\cos x)/(\cos x))/(\sin x+\cos x)`

`=(\sin x+\cos x)/(\cos x) * (1)/(\sin x+\cos x)`

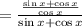
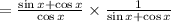
Cancelling the common terms (sinx + cosx)

`=(1)/(c o s x)`

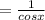
We know secant is inverse of cosine

`=\sec x=R . H . S`

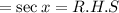
Thus L.H.S = R.H.S

`(1+\tan x)/(\sin x+\cos x)=\sec x`

Hence proved