Question

Which expression is equivalent to (x^6×x^10/×^-3)^2 and why?

Answer 1

The solution for the given expression is
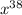`x^(38)` , i.e option C

Explanation:

Given expression as :

`((x^(6)* x^(10))/(x^(-3)))^(2)`

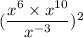
Now, From the common radix method

∵ In multiplication of radix , if the radix is same , then power is added

I.e
`x^(6)* x^{10` =
`x^(6+10)`

Or ,
`x^(6)* x^{10` =
`x^(16)`

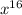
Now, The expression can be written as

`((x^(16))/(x^(-3)))^(2)`

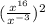
And In Division of radix , if the radix is same , then power is subtracted

So,
`(x^(16))/(x^(-3))`

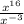
Or,
`x^(16 - (-)3)`

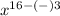
Or,
`x^(16 + 3)`

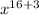
or,
`x^(19)`

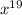
∴ The expression is now

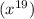`(x^(19))`²

Now, again this is written as

`x^(19)` ×
`x^(19)`

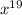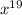
I.e here again the radix is same and in multiple for, so, power is added

∴
`x^(19)` ×
`x^(19)` =
`x^(19+19)`

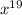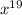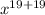
I.e
`x^(19)` ×
`x^(19)` =
`x^(38)`

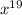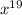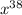
Hence The solution for the given expression is
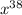`x^(38)` , i.e option C . Answer