Question

Solve the following exponential equation by taking the natural logarithm on both sides. Express the solution in terms of natural logarithms Then. use a calculate obtain a decimal approximation for the solution. e^2 - 4x = 662

What is the solution in terms of natural logarithms?
The solution set is { }.
(Use a comma to separate answers as needed. Simplify your answer Use integers or fractions for any numbers in expression).
What is the decimal approximation for the solution?
The solution set is { }.
(Use a comma to separate answers as needed. Round to two decimal places as needed.)

Answer 1

`-(ln(662)-2)/(4)`

{-1.12}

Explanation:

`e^(2 - 4x) = 662`

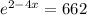
Solve this exponential equation using natural log

Take natural log ln on both sides

`ln(e^(2 - 4x)) = ln(662)`

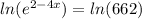
As per the property of natural log , move the exponent before log

`2-4x(ln e) = ln(662)`

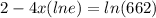
we know that ln e = 1

`2-4x= ln(662)`

Now subtract 2 from both sides

`-4x= ln(662)-2`

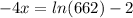
Divide both sides by -4

`x=-(ln(662)-2)/(4)`

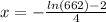
Solution set is {
`x=-(ln(662)-2)/(4)`}

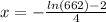USe calculator to find decimal approximation

x=-1.12381x=-1.12