Question

In rhombus MOTH, angle HTM=(5x+6) degrees. If angle HMO=(12x-6)degrees, what is angle HMO?

Answer 1

m∠HMO=102°

Explanation:

we know that

In a Rhombus the diagonals bisect the angles and opposite angles are equal

In this problem

Angles HMO and HTO are opposite angles

m∠HMO=m∠HTO

m∠HTM=(1/2)m∠HMO ----> because the diagonals bisect the angles and opposite angles are congruent

substitute the values

`(5x+6)\°=(1/2)(12x-6)\°`

solve for x

`10x+12=12x-6\\12x-10x=12+6\\2x=18\\x=9`

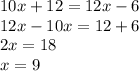
Find the measure of angle HMO

m∠HMO=(12x-6)°

substitute the value of x

m∠HMO=(12(9)-6)=102°

see the attached figure to better understand the problem