Question

g My Notes Water flows from the bottom of a storage tank at a rate of r(t) = 200 − 4t liters per minute, where 0 ≤ t ≤ 50. Find the amount of water that flows from the tank during the first 30 minutes. 4400 Incorrect: Your answer is incorrect. liters

Answer 1

4,200 liters

Explanation:

The flow rate is given by:

`r(t) = 200 - 4t`

Integrating the flow rate expression from t=0 to t=30 minutes, yields the total volume that flows out of the tank during that period:

`\int\limits^(30)_0 {r(t)} = \int\limits^(30)_0 {(200 - 4t} )\, dt \\V=(200t - 2t^2)|_0^(30)\\V= (200*30 -2*30^2)-(200*0 -2*0^2)\\V=4,200\ liters`

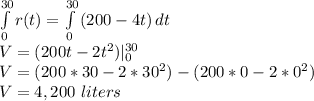
4,200 liters of water flow from the tank during the first 30 minutes.