Question

During a solar eclipse, the Moon is positioned directly between Earth and the Sun. Find the magnitude of the net gravitational force acting on the Moon during the solar eclipse due to both Earth and the Sun.

Answer 1

`F_(resultant) = 2.373* 10^(20)\ N`

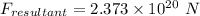
Solution:

As per the question:

We know that:

Mass of the moon,
`M_(m) = 7.36* 10^(22)\ kg`

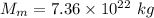
Mass of the Earth,
`M_(e) = 5.98* 10^(24)\ kg`

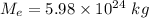
Mass of the sun,
`M_(s) = 1.99* 10^(30)\ kg`

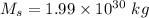
Mean distance between the Earth and the sun, R =
`1.5* 10^(11)\ m`

Mean distance between the Earth and the moon, R' =
`3.84* 10^(8)\ m`

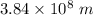
Now,

We know that the gravitational force is given by:

`F = (GMm)/(r^(2))`

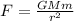
Thus

Gravitational force between the Earth and the Moon:

`F_(em) = (6.67* 10^(- 11)* 5.98* 10^(30)* 7.36* 10^(22))/((3.84* 10^(8))^(2))`

`F_(em) = 1.9908* 10^(20)\ N`

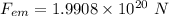
The above force is towards the earth:

The force of gravitation between the sun and moon:

`F_(sm) = (6.67* 10^(- 11)* 1.99* 10^(30)* 7.36* 10^(22))/((1.5* 10^(11) - 3.84* 10^(8))^(2))`

`F_(sm) = 4.364* 10^(20)\ N`

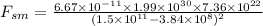
Thus net force is given by:

`F_(resultant) = F_(sm) - F_(em) = 4.364* 10^(20) - 1.9908* 10^(20) = 2.373* 10^(20)\ N`

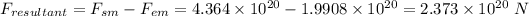
The resultant force is directed towards the sun.