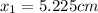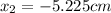Question

we must apply a force of magnitude 83 N to hold the block stationary at x = −2.0 cm. From that position we then slowly move the block so that our force does +4.8 J of work on the spring-block system; the block is then again stationary. What is the block's position x? (There are two answers.)

Answer 1

The concept required to develop this problem is Hook's Law and potential elastic energy.

By definition the force by Hooke's law is defined as

`F = kx`

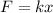
Where,

k = Spring Constant

x = Displacement

On the other hand, the elastic potential energy is defined as

`E = (1)/(2) k\Delta x^2`

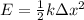
With the given values we can find the value of the spring constant, that is,

`F = kx`

`k=(F)/(x)`

`k= (83)/(0.02)`

`k = 4120N/m`

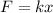
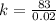
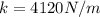
Applying the concepts of energy conservation then we can find the position of the block, that is,

`E = (1)/(2) k\Delta x^2`

`E = (1)/(2) k\Delta x^2`

`4.8 = (1)/(2) (4120)(x^2-(-0.02)^2)`

`x = \sqrt{(2*4.8)/(4120)+(-0.02)^2}`

`x = \pm 0.05225m`

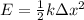
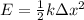
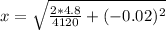
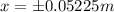
Therefore the position of the block can be then,

`x_1 = 5.225cm`

`x_2 = -5.225cm`