Answer: B. 461 acres
Explanation:
Given : In an agricultural study, the average amount of corn yield is normally distributed with a mean of 185.2 bushels of corn per acre, with a standard deviation of 23.5 bushels of corn.
i.e.
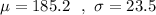
Let x denotes the amount of corn yield.
Now, the probability that the amount of corn yield is more than 190 bushels of corn per acre.
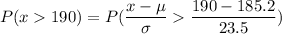
[Formula :
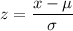 ]
]
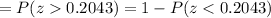 [∵ P(Z>z)=1-P(Z<z)]
[∵ P(Z>z)=1-P(Z<z)]
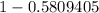 [using z-value calculator or table]
[using z-value calculator or table]
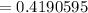
Now, If a study included 1100 acres then the expected number to yield more than 190 bushels of corn per acre :-
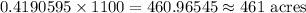
hence, the correct answer is B. 461 acres .