Question

Two waves traveling on a string in the same direction both have a frequency of 135 Hz, a wavelength of 2 cm, and an amplitude of 0.04 m. What is the amplitude of the resultant wave if the original waves differ in phase by each of the following values?

(a) p/6 cm(b) p/3 cm

Answer 1

The amplitude of the resultant wave are

(a). 0.0772 m

(b). 0.0692 m

Step-by-step explanation:

Given that,

Frequency = 135 Hz

Wavelength = 2 cm

Amplitude = 0.04 m

We need to calculate the angular frequency

`\omega=2\pi f`

`\omega=2*\pi*135`

`\omega=848.23\ rad/s`

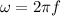
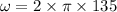
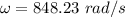
As the two waves are identical except in their phase,

The amplitude of the resultant wave is given by

`y+y=A\sin(kx-\omega t)+Asin(kx-\omega t+\phi)`

`y+y=A[2\sin(kx-\omega t+(\phi)/(2))\cos\phi(\phi)/(2)`

`y'=2A\cos((\phi)/(2))\sin(kx-\omega t+(\phi)/(2))`

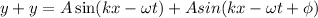
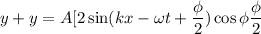
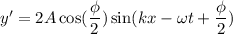
(a). We need to calculate the amplitude of the resultant wave

For
`\phi =(\pi)/(6)`

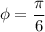
The amplitude of the resultant wave is

`A'=2A\cos((\phi)/(2))`

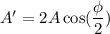
Put the value into the formula

`A'=2*0.04\cos((\pi)/(12))`

`A'=0.0772\ m`

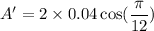
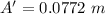
(b), We need to calculate the amplitude of the resultant wave

For
`\phi =(\pi)/(3)`

`A'=2*0.04\cos((\pi)/(6))`

`A'=0.0692\ m`

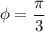
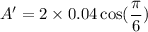
Hence, The amplitude of the resultant wave are

(a). 0.0772 m

(b). 0.0692 m