Question

The nearest known exoplanets (planets beyond the solar system) are around 20 light-years away. What would have to be the minimum diameter of an optical telescope to resolve a Jupiter-sized planet at that distance using light of wavelength 600 nm? (Express your answer to two significant figures.)

Answer 1

To solve the problem, it is necessary to apply the concepts related to the diffraction given in circular spaces. By definition it is expressed as

`\Delta \theta = 1.22(\lambda)/(d)`

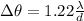
Where,

\lambda = Wavelength

d = Optical Diameter

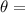`\theta =` Angular resolution

In turn you can calculate the angle through the diameter and the arc length, that is,

`\Delta \theta = (x)/(D)`

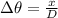
Where,

x = The length of the arc

D = Distance

From known data we know that Jupiter's diameter is,

`x_J = 1.43*10^8m`

`D = 20*9.4608*10^(15)`

`\lambda = 600*10^(-9)m`

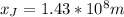
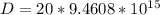
Replacing we have that,

`(x)/(D) = 1.22(\lambda)/(d)`

`(1.43*10^8)/(20*9.4608*10^(15) ) = 1.22(600*10^(-9))/(d)`

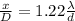
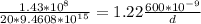
Re-arrange to find d,

`d = 968.5m = 0.968Km`

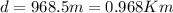
Therefore the minimum diameter of an optical telescope to resolve a Jupiter-sized planet is 0.968Km.