Question

Interactive LearningWare 10.1 reviews the concepts involved in this problem. A spring stretches by 0.0161 m when a 3.74-kg object is suspended from its end. How much mass should be attached to this spring so that its frequency of vibration is f = 3.84 Hz?

Answer 1

m = 3.91 kg

Step-by-step explanation:

Given that,

Mass of the object, m = 3.74 kg

Stretching in the spring, x = 0.0161 m

The frequency of vibration, f = 3.84 Hz

When the object is suspended, the gravitational force is balanced by the spring force as :

`mg=kx`

`k=(mg)/(x)`

`k=(3.74* 9.8)/(0.0161)`

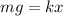
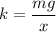
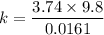
k = 2276.52 N/m

The frequency of vibration is given by :

`f=(1)/(2\pi)\sqrt{(k)/(m)}`

`m=(k)/(4\pi^2f^2)`

`m=(2276.52)/(4\pi^2* (3.84)^2)`

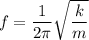
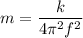
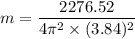
m = 3.91 kg

So, the mass of the object is 3.91 kg. Hence, this is the required solution.