Question

An inspector inspects large truckloads of potatoes to determine the proportion p in the shipment with major defects prior to using the potatoes to make potato chips. If there is clear evidence that this proportion is less than 0.10, she will accept the shipment. To reach a decision, she will test the hypotheses H0: p = 0.10, Ha: p < 0.10. To do so, she selects a simple random sample of 150 potatoes from the more than 3000 potatoes on the truck. Only eight of the potatoes sampled are found to have major defects. What is the value of the large-sample z test statistic?

Answer 1

Answer: z=1.9065

Explanation:

As per given , we have

`H_0: p=0.10\\\\ H_a: p<0.10`

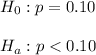
Sample size : n= 150

No. of potatoes sampled are found to have major defects = 8

The sample proportion of potatoes sampled are found to have major defects :

`\hat{p}=(8)/(150)=0.0533`

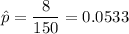
The test statistic for population proportion is given by :-

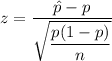`z=\frac{\hat{p}-p}{\sqrt{(p(1-p))/(n)}}\\\\` , where p=population proportion.

n= sample size.

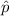`\hat{p}` = sample proportion.

`z=\frac{0.0533-0.10}{\sqrt{(0.10*0.90)/(150)}}\\\\=(-0.0467)/(0.02449)\\\\=-1.90651951647\approx1.9065`

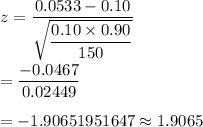
Hence, the value of the large-sample z test statistic is z=1.9065 .