Answer:
The following two equations model this relationship.
Explanation:
We know that when 'y' varies inversely with 'x', we get the equation
y ∝ 1/x
y = k / x
k = yx
where 'k' is called the 'constant of proportionality'.
In our case, it is given that the cube root of 'r' varies inversely with the square of 's', then
![\sqrt[3]{r}](https://img.qammunity.org/2022/formulas/mathematics/high-school/78b49pbulkv73kz0le78mx3hlq4cg98d98.png) ∝
∝

![\:\sqrt[3]{r}=\:(k)/(s^2)](https://img.qammunity.org/2022/formulas/mathematics/high-school/ijhe7ecx86ywnfzmn8ob7e4f2jyiooja4f.png)
or
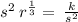 ∵
∵
![\sqrt[3]{r}=r^{(1)/(3)}](https://img.qammunity.org/2022/formulas/mathematics/high-school/fry4bbps6vliabh4o2w8sqmuopybol3mw3.png)
Therefore, the following two equations model this relationship.