Answer:

Explanation:
We have to convert an exponential equation into the logarithmic equation.
The given equation is

Now, taking log on both sides we get,

⇒

{Since we know from the logarithmic property that
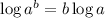 and
and
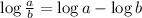 }
}
⇒
 {Since
{Since
 }
}
Hence, this is the required logarithmic equation. (Answer)