Question

Determine the ratio of the flow rate through capillary tubes A and B (that is, Qa/Qb).

The length of A is twice that of B, and the radius of A is one-half that of B.

The pressure across both tubes is the same.

Answer 1

To solve this problem we can use the concepts related to the change of flow of a fluid within a tube, which is without a rubuleous movement and therefore has a laminar fluid.

It is sometimes called Poiseuille’s law for laminar flow, or simply Poiseuille’s law.

The mathematical equation that expresses this concept is

`\dot{Q} = (\pi r^4 (P_2-P_1))/(8\eta L)`

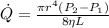
Where

P = Pressure at each point

r = Radius

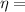`\eta =` Viscosity

l = Length

Of all these variables we have so much that the change in pressure and viscosity remains constant so the ratio between the two flows would be

`\frac{\dot{Q_A}}{\dot{Q_B}} = (r_A^4)/(r_B^4)(L_B)/(L_A)`

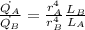
From the problem two terms are given

`R_A = (R_B)/(2)`

`L_A = 2L_B`

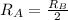
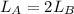
Replacing we have to

`\frac{\dot{Q_A}}{\dot{Q_B}} = (r_A^4)/(r_B^4)(L_B)/(L_A)`

`\frac{\dot{Q_A}}{\dot{Q_B}} = (r_B^4)/(16*r_B^4)(L_B)/(2*L_B)`

`\frac{\dot{Q_A}}{\dot{Q_B}} = (1)/(32)`

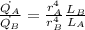
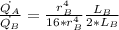
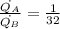
Therefore the ratio of the flow rate through capillary tubes A and B is 1/32