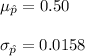Answer:
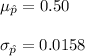
Explanation:
The probability distribution of sampling distribution
 is known as it sampling distribution.
is known as it sampling distribution.
The mean and standard deviation of the proportion is given by :-
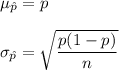
, where p =population proportion and n= sample size.
Given : According to a survey, 50% of Americans were in 2005 satisfied with their job.
i.e. p = 50%=0.50
Now, for sample size n= 1000 , the mean and standard deviation of the proportion will be :-
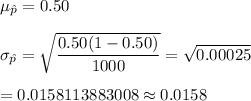
Hence, the mean and standard deviation of the proportion for a sample of 1000: