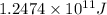Question

The sun produces energy via fusion. One of the fusion reactions that occurs in the sun is 411H→42He+201e How much energy in joules is released by the fusion of 2.01 g of hydrogen-1? Express your answer to three significant figures and include the appropriate units.

Answer 1

Answer: The energy released for the the given amount of hydrogen -1 atom is
`1.2474* 10^(11)J`

Step-by-step explanation:

First we have to calculate the mass defect
`(\Delta m)`.

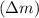The given equation follows:

`4_(1)^(1)\textrm{H}\rightarrow _(2)^(4)\textrm{He}+2_0^(1)\textrm{e}`

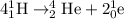
To calculate the mass defect, we use the equation:

Mass defect = Sum of mass of product - Sum of mass of reactant

`\Delta m=(2m_(e)+m_(He))-(4m_(H))`

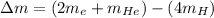
We know that:

`m_e=0.00054858g/mol\\m_(H)=1.00782g/mol\\m_(He)=4.00260g/mol`

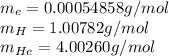
Putting values in above equation, we get:

`\Delta m=((2* 0.00054858)+4.00260)-(4* 1.00782)=-0.027583g=-2.7583* 10^(-5)kg`

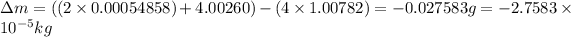
(Conversion factor: 1 kg = 1000 g )

To calculate the energy released, we use Einstein equation, which is:

`E=\Delta mc^2`

`E=(-2.7583* 10^(-5)kg)* (3* 10^8m/s)^2`

`E=-2.4825* 10^(11)J`

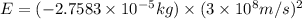
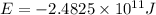
The energy released for 4 moles of hydrogen atom is
`2.4825* 10^(11)J`

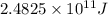
To calculate the number of moles, we use the equation:

`\text{Number of moles}=\frac{\text{Given mass}}{\text{Molar mass}}`

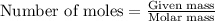
Given mass of hydrogen atom = 2.01 g

Molar mass of hydrogen atom = 1 g/mol

Putting values in above equation, we get:

`\text{Moles of hydrogen atom}=(2.01g)/(1g/mol)=2.01mol`

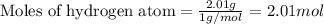
We need to calculate the energy released for the fusion of given amount of hydrogen atom. By applying unitary method, we get:

As, 4 moles of hydrogen atom releases energy of =
`2.4825* 10^(11)J`

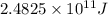
Then, 2.01 moles of hydrogen atom will release energy of =
`(2.4825* 10^(11))/(4)* 2.01=1.2474* 10^(11)J`

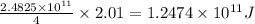
Hence, the energy released for the the given amount of hydrogen -1 atom is
`1.2474* 10^(11)J`