Question

A 1 m3 rigid tank initially contains air whose density is 1.18kg/m3. The tank is connected to a high pressure supply line througha valve. The valve is opened, and air is allowed to enter the tankuntil the density in the tank rises to 7.20 kg/m3.

Determine themass of air that has entered the tank.

Answer 1

To solve this problem it is necessary to apply the concepts related to density in relation to mass and volume for each of the states presented.

Density can be defined as

`\rho = (m)/(V)`

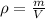
Where

m = Mass

V = Volume

For state one we know that

`\rho_1 = (m_1)/(V)`

`m_1 = \rho_1 V`

`m_1 = 1.18*1`

`m_1 = 1.18Kg`

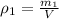
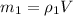
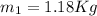
For state two we have to

`\rho_2 = (m_2)/(V)`

`m_2 = \rho_2 V`

`m_1 = 7.2*1`

`m_1 = 7.2Kg`

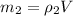
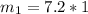
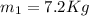
Therefore the total change of mass would be

`\Delta m = m_2-m_1`

`\Delta m = 7.2-1.18`

`\Delta m = 6.02Kg`

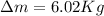
Therefore the mass of air that has entered to the tank is 6.02Kg