Question

The average GRE score at the University of Pennsylvania for the incoming class of 2016-2017 was 311. Assume that the standard deviation was 13.

If you select a random sample of 40 students, what is the probability that the sample mean will be greater than 308? Round your answer to three decimal places.

Answer 1

`P(\bar X>308)=1-0.0721=0.928`

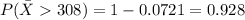
Explanation:

1) Previous concepts

Normal distribution, is a "probability distribution that is symmetric about the mean, showing that data near the mean are more frequent in occurrence than data far from the mean".

The Z-score is "a numerical measurement used in statistics of a value's relationship to the mean (average) of a group of values, measured in terms of standard deviations from the mean".

Let X the random variable that represent the GRE score at the University of Pennsylvania for the incoming class of 2016-2017, and for this case we know the distribution for X is given by:

`X \sim N(\mu=311,\sigma=13)`

And let
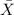`\bar X` represent the sample mean, the distribution for the sample mean is given by:

`\bar X \sim N(\mu,(\sigma)/(√(n)))`

On this case
`\bar X \sim N(311,(13)/(√(40)))`

2) Calculate the probability

We want this probability:

`P(\bar X>308)=1-P(\bar X<308)`

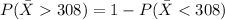
The best way to solve this problem is using the normal standard distribution and the z score given by:

`z=(x-\mu)/((\sigma)/(√(n)))`

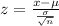
If we apply this formula to our probability we got this:

`P(\bar X >308)=1-P(Z<(308-311)/((13)/(√(40))))=1-P(Z<-1.46)`

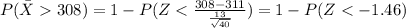
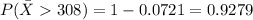`P(\bar X>308)=1-0.0721=0.9279` and rounded would be 0.928