Find the equation of the line in slope-intercept form (-1,-1) and (1,0)

Question

asked Oct 6, 2022 201k views

1 Answer

Mre · Answer 1 · 2022-10-10T13:38:11+0000

Answer:

An equation in slope-intercept form of the line will be

Explanation:

The slope-intercept form of the line equation

y = mx+b

where m is the slope and b is the y-intercept

Given the points

Finding the slope between (-1,-1) and (1,0)

$\mathrm{Slope}=(y_2-y_1)/(x_2-x_1)$

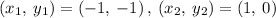
$\left(x_1,\:y_1\right)=\left(-1,\:-1\right),\:\left(x_2,\:y_2\right)=\left(1,\:0\right)$

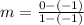
$m=(0-\left(-1\right))/(1-\left(-1\right))$

m=(1)/(2)

substituting m = 1/2 and (-1, -1) in the slope-intercept form of the line equation to determine the y-intercept

y = mx+b

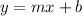
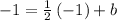
$-1=(1)/(2)\left(-1\right)+b$

-(1)/(2)+b=-1

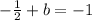
Add 1/2 to both sides

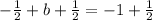
-(1)/(2)+b+(1)/(2)=-1+(1)/(2)

b=-(1)/(2)

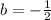
substituting m = 1/2 and b = -1/2 in the slope-intercept form of the line equation

y = mx+b

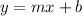
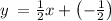
$y\:=(1)/(2)x+\left(-(1)/(2)\right)$

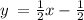
$y\:=(1)/(2)x-(1)/(2)$

Therefore, an equation in slope-intercept form of the line will be