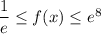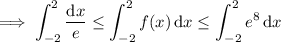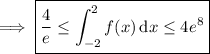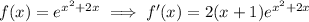
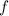 has critical points where the derivative is 0:
has critical points where the derivative is 0:
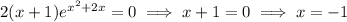
The second derivative is
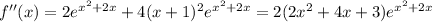
and
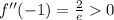 , which indicates a local minimum at
, which indicates a local minimum at
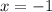 with a value of
with a value of
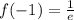 .
.
At the endpoints of [-2, 2], we have
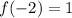 and
and
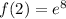 , so that
, so that
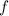 has an absolute minimum of
has an absolute minimum of
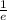 and an absolute maximum of
and an absolute maximum of
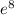 on [-2, 2].
on [-2, 2].
So we have