Answer : The value of
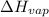 is 28.97 kJ/mol
is 28.97 kJ/mol
Explanation :
To calculate
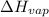 of the reaction, we use clausius claypron equation, which is:
of the reaction, we use clausius claypron equation, which is:
![\ln((P_2)/(P_1))=(\Delta H_(vap))/(R)[(1)/(T_1)-(1)/(T_2)]](https://img.qammunity.org/2020/formulas/chemistry/college/4vtbgz8qequ3vvsclhkmmvxlsikmj2gcnu.png)
where,
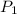 = vapor pressure at temperature
= vapor pressure at temperature
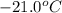 = 462.7 mmHg
= 462.7 mmHg
 = vapor pressure at temperature
= vapor pressure at temperature
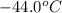 = 140.5 mmHg
= 140.5 mmHg
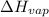 = Enthalpy of vaporization = ?
= Enthalpy of vaporization = ?
R = Gas constant = 8.314 J/mol K
 = initial temperature =
= initial temperature =
![-21.0^oC=[-21.0+273]K=252K](https://img.qammunity.org/2020/formulas/chemistry/high-school/91yil3pne2w8pysrfuq1tla6bjbdz0e43q.png)
 = final temperature =
= final temperature =
![45^oC=[-41.0+273]K=232K](https://img.qammunity.org/2020/formulas/chemistry/high-school/u7zmh95bws63vmlhokgcd5qxmgvbz84vlp.png)
Putting values in above equation, we get:
![\ln((140.5mmHg)/(462.7mmHg))=(\Delta H_(vap))/(8.314J/mol.K)[(1)/(252)-(1)/(232)]\\\\\Delta H_(vap)=28966.6J/mol=28.97kJ/mol](https://img.qammunity.org/2020/formulas/chemistry/high-school/hbj3jnrewds6pgsfj429g9c5n494zr1g43.png)
Therefore, the value of
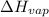 is 28.97 kJ/mol
is 28.97 kJ/mol