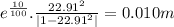Question

An electric motor has an eccentric mass of 10 kg (10% of the total mass) and is set on two identical springs (k=3200 N/m). The motor runs at 1750 rpm, and the mass eccentricity is 100 mm from the center. The springs are mounted 250 mm apart with the motor shaft in the center. Neglect damping and determine the amplitude of vertical vibration.

Answer 1

The amplitude is 0.010 m

Solution:

As per the question:

Eccentric Mass,
`m_(e) = 10\ kg`

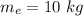
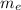`m_(e)` = 10%M kg

0.1M = 10

Total mass, M = 100 kg

Spring constant, k = 3200 N/m

Eccentric center, e = 100 mm = 0.1 m

Speed of motor, N = 1750 rpm

Distance between two springs, d = 250 mm = 0.25 m

Now,

Angular velocity,
`\omega = (2\pi N)/(60) = (2\pi * 1750)/(60) = 183.26\ rad/s`

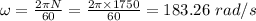
For the vertical vibrations:

`\omega_(n) = \sqrt{(2k)/(M)} = \sqrt{(6400)/(100)} = 8\ rad/s`

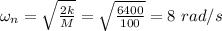
Now, the frequency ratio is given by:

r =
`(\omega)/(\omega_(n)) = (183.26)/(8) = 22.91`

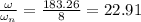
Thus the amplitude is given by:

A =
`e^{(m_(e))/(M)}.(r^(2))/(|1 - r^(2)|)`

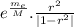
A =
`e^{(10)/(100)}.(22.91^(2))/(|1 - 22.91^(2)|) = 0.010 m`