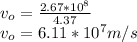Answer:
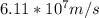
Step-by-step explanation:
The Doppler effect formula for an observer approaching a source is given by equation (1);
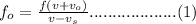
where
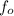 is the frequency perceived by the observer, v is the actual velocity of the wave in air,
is the frequency perceived by the observer, v is the actual velocity of the wave in air,
 is the velocity of the observer,
is the velocity of the observer,
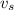 is the velocity of the source and
is the velocity of the source and
 is the actual frequency of the wave.
is the actual frequency of the wave.
The actual velocity v of light in air is
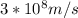 . The relationship between velocity, frequency and wavelength
. The relationship between velocity, frequency and wavelength
 is given by equation (2);
is given by equation (2);

therefore;

We therefore use equation (3) to find the actual frequency of light emitted and the frequency perceived by Slick Willy.
Actual wavelength
 of light emitted is 678nm, hence actual frequency is
of light emitted is 678nm, hence actual frequency is
given by;
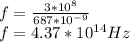
Also, the frequency perceived by Slick Willy is given thus;
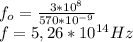
The velocity
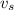 of the source light is zero since the traffic light was stationary. Substituting all parameters into equation (1), we obtain the following;
of the source light is zero since the traffic light was stationary. Substituting all parameters into equation (1), we obtain the following;

We then simplify further to get

 cancels out from both sides, so we obtain the following;
cancels out from both sides, so we obtain the following;
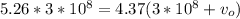
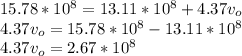
Hence;