Question

A survey of 865 voters in one state reveals that 408 favor approval of an issue before the legislature.

Construct the 95 % confidence interval for the true proportion of all voters in the state who favor approval.

A) 0.435 < p < 0.508

B) 0.444 < p < 0.500

C) 0.471 < p < 0.472

D) 0.438 < p < 0.505

Answer 1

Answer: D) 0.438 < p < 0.505

Explanation:

We know that the confidence interval for population proportion is given by :-

`\hat{p}\pm z^*\sqrt{\frac{\hat{p}(1-\hat{p})}{n}}`

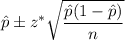
, where n= sample size

`\hat{p}` = Sample proportion.

z* = critical value.

Given : A survey of 865 voters in one state reveals that 408 favor approval of an issue before the legislature.

i.e. n= 865

`\hat{p}=(408)/(865)\approx0.4717`

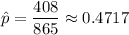
Two-tailed critical avlue for 95% confidence interval : z* = 1.96

Then, the 95 % confidence interval for the true proportion of all voters in the state who favor approval will be :-

`0.4717\pm (1.96)\sqrt{(0.4717(1-0.4717))/(865)}\\\\\approx0.4717\pm 0.03327\\\\=(0.4717-0.03327,\ 0.4717+0.03327)=(0.43843,\ 0.50497)\approx(0.438,\ 0.505)`

Thus, the required 95% confidence interval : (0.438, 0.505)

Hence, the correct answer is D) 0.438 < p < 0.505