Question

The manager of a movie theater found that Saturdays sales were $3675. He knew that a total of 650 tickets were sold on saturday. Adult tickets cost $7.50, and children tickets cost $4.50. How many of each kind of ticket were sold?

Answer 1

Adults= 250 tickets

Children= 400 tickets

Explanation:

Answer 2

250 adult tickets were sold and 400 children tickets were sold

Step by Step Explanation:

Given

Saturday Sales: $3675

Total tickets: 650

Cost of adult tickets = $7.50

Cost of children tickets = $4.50

Let A represent the adult tickets and C represent the children tickets,

if there's a total of 650 tickets, then

A + C = 650

Also,

if an adult ticket cost $7.50 and a child ticket cost $4.50 then

7.5A + 4.5C = 3675

From these, we have a simultaneous equation

A + C = 650 ------- (1)

7.5A + 4.5C = 3675 ----------(2)

Make A the subject of formula in (1)

A + C = 650 becomes

A = 650 - C

Substitute 650 - C for A in (2), we have

7.5(650 - C) + 4.5C = 3675

Open the bracket

4875 - 7.5C + 4.5C = 3675

4875 - 3C = 3675

Collect like terms

-3C = 3675 - 4875

-3C = -1200

Divide through by -3

`(-3C)/(-3) = (-1200)/(-3)`

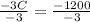
C = 400

Recall that

A = 650 - C

So, A = 650 - 400

A = 250

Hence, 250 adult tickets were sold and 400 children tickets were sold