Answer:
OPTION A and OPTION C
Explanation:
OPTION A:
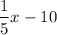 and
and
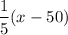
Consider
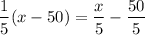
This is equal to
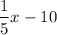 .
.
This is exactly the first expression. So, we say both expressions are equivalent.
OPTION B:
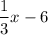 and
and
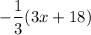
Distributing
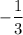 to
to
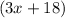 we get:
we get:
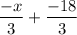
⇒
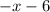
This is not equivalent to the first expression.
OPTION C:
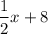 and
and
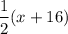
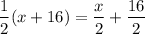
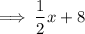
This is exactly the first expression. So, we say the expressions are equal.
We apply similar techniques to OPTION D and OPTION E. Note that the expressions are not equal in both the options.