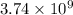Question

The radius of the aorta is «10 mm and the blood flowing through it has a speed of about 300 mm/s. A capillary has a radius of about 4ˆ10´3 mm but there are literally billions of them. The average speed of blood through the capillaries is about 5ˆ10´4 m/s. (i) Calculate the effective cross sectional area of the capillaries and (ii) the approximate number of capillaries.

Answer 1

(I). The effective cross sectional area of the capillaries is 0.188 m².

(II). The approximate number of capillaries is
`3.74*10^(9)`

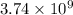
Step-by-step explanation:

Given that,

Radius of aorta = 10 mm

Speed = 300 mm/s

Radius of capillary
`r=4*10^(-3)\ mm`

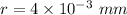
Speed of blood
`v=5*10^(-4)\ m/s`

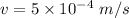
(I). We need to calculate the effective cross sectional area of the capillaries

Using continuity equation

`A_(1)v_(1)=A_(2)v_(2)`

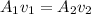
Where. v₁ = speed of blood in capillarity

A₂ = area of cross section of aorta

v₂ =speed of blood in aorta

Put the value into the formula

`A_(1)=A_(2)*(v_(2))/(v_(1))`

`A_(1)=\pi*(10*10^(-3))^2*(300*10^(-3))/(5*10^(-4))`

`A_(1)=0.188\ m^2`

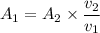
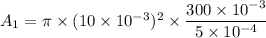
(II). We need to calculate the approximate number of capillaries

Using formula of area of cross section

`A_(1)=N\pi r_(c)^2`

`N=(A_(1))/(\pi* r_(c)^2)`

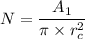
Put the value into the formula

`N=(0.188)/(\pi*(4*10^(-6))^2)`

`N=3.74*10^(9)`

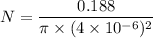
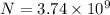
Hence, (I). The effective cross sectional area of the capillaries is 0.188 m².

(II). The approximate number of capillaries is
`3.74*10^(9)`