The equation of line perpendicular to line containing points (-3, 4) and (1, 0) and passes through (-2, 6) in point slope form is y = x + 8
Solution:
Given that line m contains points (-3, 4) and (1, 0)
We are asked to find the equation of line perpendicular to line containing points (-3, 4) and (1, 0) and passes through (-2, 6)
Let us first find slope of the line "m"
Given two points are (-3, 4) and (1, 0)

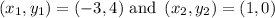
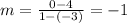
Thus slope of line m is -1
We know that product of slope of given line and perpendicular line are always -1
So, we get

So we have got the slope of perpendicular line is 1 and it passes through (-2, 6)
Let us use the point slope form to find the required equation
The point slope form is given as:
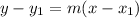
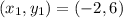 and m = 1
and m = 1
y - 6 = 1(x - (-2))
y - 6 = x + 2
y = x + 8
Thus equation of required line in point slope form is y = x + 8