Answer: 95% confidence interval would be (0.344,0.456).
Explanation:
Since we have given that
n = 295
x = 118
so,
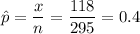
At 95% confidence, z = 1.96
So, margin of error would be
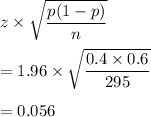
so, 95% confidence interval would be

Hence, 95% confidence interval would be (0.344,0.456).