Question

Ask Your Teacher Calculate the freezing-point depression and osmotic pressure in torr at 25°C for an aqueous solution of 3.2 g/L of a protein (molar mass = 9.0 ✕ 104 g/mol) if the density of the solution is 1.0 g/cm3

Answer 1

Osmotic pressure(π) = 0.661 Torr.

Depression in freezing point = 6.64 * 10⁻⁵ °C.

Step-by-step explanation:

To calculate depression in freezing point and osmotic pressure, let's start by calculating Molarity of the solution.

Also, protein undergoes no dissociation or association when in solution.

Molarity =
`(Moles of solute)/(liters of solution)`

Molarity =
`(3.2 g/L)/(9.0 * 10^(4)g/mol )`

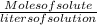
Molarity= 3.56 * 10⁻⁵ mol/L

Temperature = 25 +273 = 298 K

Osmotic pressure(π) = M R T

= (3.56 * 10⁻⁵ mol/L)* (0.08206 L atm/ mol K) * (298 K)

= 87.055 * 10⁻⁵ atm

But 1 atm= 760 Torr

So, Osmotic pressure(π) = (87.055 * 10⁻⁵ atm) * ( 760 torr/ 1atm)

= 0.661 Torr.

The depression in freezing point Δ
`T_(f) =K_(f) * m`

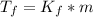
`K_(f)`= molal freezing point depression constant of the solvent (1.86 °C/m for water).

m= molality or molal concentration of the solution.

m= moles of solute in 1kg of solvent.

Density of solution =
`1.0 (g)/(cm^(3) )`

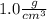
Mass of 1L(1000 cm³) of this solution is= density * volume of solution

= 1000g

Molarity means 3.56 * 10⁻⁵ mol of protein in 1L of solution

Mass of protein= 3.56 * 10⁻⁵ * 9.0 * 10⁴ = 3.2 g of protein

1000g of solution- 3.2 g of protein = 996.8 g of solvent

Molality =
`(3.56 * 10⁻⁵ mol)/(0.9968 kg)`

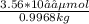
=3.57 * 10⁻⁵ m

depression in freezing point Δ
`T_(f) =K_(f) * m`

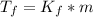
= 1.86 * 3.57 * 10⁻⁵ = 6.64 * 10⁻⁵ °C.