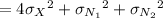a.
 ,
,
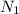 , and
, and
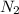 each have mean 0, and by linearity of expectation we have
each have mean 0, and by linearity of expectation we have
![E[R_1]=E[X+N_1]=E[X]+E[N_1]=0](https://img.qammunity.org/2020/formulas/mathematics/college/fblcscy7zwul5j4240447sr63be4jh6esh.png)
![E[R_2]=E[X+N_2]=E[X]+E[N_2]=0](https://img.qammunity.org/2020/formulas/mathematics/college/tb4j6rle8fhed1976l04ap89ia2bv3jo3t.png)
b. By definition of correlation, we have
![\mathrm{Corr}[R_1,R_2]=\frac{\mathrm{Cov}[R_1,R_2]}{{\sigma_(R_1)}{\sigma_(R_2)}}](https://img.qammunity.org/2020/formulas/mathematics/college/5kd3p0e9fkicywg5l7wexpvjl9yujq9yjk.png)
where
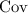 denotes the covariance,
denotes the covariance,
![\mathrm{Cov}[R_1,R_2]=E[(R_1-E[R_1])(R_2-E[R_2])]](https://img.qammunity.org/2020/formulas/mathematics/college/sxumpzbm0gobunlv9g57gg4s3fnac2m3uq.png)
![=E[R_1R_2]-E[R_1]E[R_2]](https://img.qammunity.org/2020/formulas/mathematics/college/sn1wvqe1ttn0e2oviib0hdidbcp5mahw4k.png)
![=E[R_1R_2]](https://img.qammunity.org/2020/formulas/mathematics/college/ud2jbrmzg1r9g5zuc9wx2vrpcb031k4mfn.png)
![=E[(X+N_1)(X+N_2)]](https://img.qammunity.org/2020/formulas/mathematics/college/43veh26sptceb8gje5pef6n5z66ge31ff2.png)
![=E[X^2]+E[N_1X]+E[XN_2]+E[N_1N_2]](https://img.qammunity.org/2020/formulas/mathematics/college/qsfp9amfeiempuzbcnivozrkwxr0ws7ziv.png)
Because
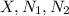 are mutually independent, the expectation of their products distributes over the factors:
are mutually independent, the expectation of their products distributes over the factors:
![\mathrm{Cov}[R_1,R_2]=E[X^2]+E[N_1]E[X]+E[X]E[N_2]+E[N_1]E[N_2]](https://img.qammunity.org/2020/formulas/mathematics/college/9slp3npwbw747m4lpxcuteuzghouru672n.png)
![=E[X^2]](https://img.qammunity.org/2020/formulas/mathematics/college/rygirv5ukc8dfnm0b4md687womge0puzch.png)
and recall that variance is given by
![\mathrm{Var}[X]=E[(X-E[X])^2]](https://img.qammunity.org/2020/formulas/mathematics/college/oud837kuyvv228jecvogd4k7dye721z9fp.png)
![=E[X^2]-E[X]^2](https://img.qammunity.org/2020/formulas/mathematics/college/g1lizsdh5kvl07kh05r4ct70seiqugso7e.png)
so that in this case, the second moment
![E[X^2]](https://img.qammunity.org/2020/formulas/mathematics/college/7sj9bplkk851agvl7azqc4gou6ln55wkie.png) is exactly the variance of
is exactly the variance of
 ,
,
![\mathrm{Cov}[R_1,R_2]=E[X^2]={\sigma_X}^2](https://img.qammunity.org/2020/formulas/mathematics/college/7p5teh2ori9jmxblvf4by8hawqpr1wfny9.png)
We also have
![{\sigma_(R_1)}^2=\mathrm{Var}[R_1]=\mathrm{Var}[X+N_1]=\mathrm{Var}[X]+\mathrm{Var}[N_1]={\sigma_X}^2+{\sigma_(N_1)}^2](https://img.qammunity.org/2020/formulas/mathematics/college/h0d6p4301uo6pnd0kwn954qok6rir6srnn.png)
and similarly,
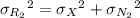
So, the correlation is
![\mathrm{Corr}[R_1,R_2]=\frac{{\sigma_X}^2}{\sqrt{\left({\sigma_X}^2+{\sigma_(N_1)}^2\right)\left({\sigma_X}^2+{\sigma_(N_2)}^2\right)}}](https://img.qammunity.org/2020/formulas/mathematics/college/nf06tg30qus7tmhs1ev8xmuzzehwm7qm0i.png)
c. The variance of
 is
is
![{\sigma_(R_1+R_2)}^2=\mathrm{Var}[R_1+R_2]](https://img.qammunity.org/2020/formulas/mathematics/college/3vidw3t1oa6jw912zvnknrxhpspxtymzgh.png)
![=\mathrm{Var}[2X+N_1+N_2]](https://img.qammunity.org/2020/formulas/mathematics/college/g2u9xqls3dh7dlq3dh59c4ef5br3mw2389.png)
![=4\mathrm{Var}[X]+\mathrm{Var}[N_1]+\mathrm{Var}[N_2]](https://img.qammunity.org/2020/formulas/mathematics/college/284qbhgizjx2tzojc744t5yg92umu8b02r.png)